42
How is it possible to sail from the UK to New Zealand along a very nearly straight line without intercepting any landmasses?
(hexbear.net)
It's a Bluesky link but he use adult tags as de facto "spoiler" tags. The problem is that content is hidden if you're not logged into Bluesky. Here's a Bluesky mirror site to show the entire thread...
https://subium.com/profile/c0nc0rdance.bsky.social/post/3kpkcq2ecws22
A huge hint...
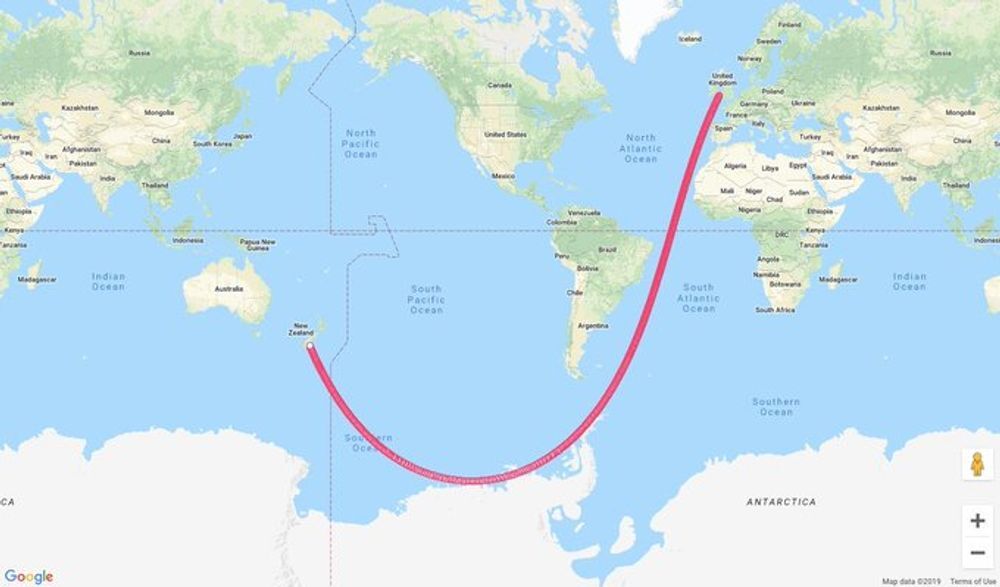
How is that nearly straight? They go South but then turn North past Tierra del Fuego.
As I understand it - it's a straight line if you had a globe and you used a piece of string.
The problem is that "straight" on the surface of a globe is a curve. The map projection (how you flatten out a globe) makes that look even weirder no matter how it is done. Is any route on the surface of a globe a straight line? Does the initial question even make sense?
Of course you can have a straight line on a globe, pick a point and walk in one direction. Eventually you'll pass a point at which your distance to a pole starts to increase again but that doesn't mean the line isn't straight.
The line might not be straight in the ambient 3d space but on the 2d surface it is.
My point is that exactly. We live and move in 3D space, so the line has to be judged in 3 dimensions. You might as well say any curved line on a 2D map looks curved, but if you look at it in 1D it is perfectly straight
No we dont live in a 3d space. That's a mathematical model used to model reality so as to be able to ignore details deemed unecessary for whatever the model is for. It's a tool to approximate reality not reality itself.
And for the purposes of traversing our globe a 3rd dimension is unecessary so why include that in your model?
And even if, its blatantly obvious that the OOP is asking for a straight line in a 2d perspective, not on a map, but on the globe itself because any projection of a globe into a flat space will take the straightness out of a straight line.
How would you begin to describe points in the spaces we are discussing? I feel this is a fair question, because in an earlier reply you suggest to picking a point and walking there.
For the surface of a sphere, the most natural way many people would choose to do this would be using the tuples (x,y,z) in R^3^ and restricting this space to a subspace by the equation X^2^ + Y^2^ + Z^2^ = r^2^, were r is the radius of the sphere. Give a model which can describe points and lines on the surface of a sphere with less than 3 dimensions; i.e., define a space for the surface of a sphere with fewer than 3 dimensions.
The problems with trying to do this by defining a conformal map from 2 dimensional projective spaces to 3 dimensional surfaces is the reason whole books are written about projective geometry.
This doesn't make sense. Which projection? The natural one? Such a map is guaranteed to not be a bijection and is potentially not well-defined. Without a clear way of doing this map, you can't say anything about what happens to lines under the image of such a map.
I agree with this at least, I too am tired of the mathematical platonism dominating the public discourse.
latitude and longitude
just put the poles wherever it's convenient
idk, to me this is kinda semantics, whether or not we say a 2d surface in 3d space is 2d or 3d.
just assume "straight line" refers to a geodesic on the surface, then you can use whatever coordinates you want.
TL;DR being able to talk about curvature in a mathematical way outside of a euclidean space is a chore because it needs differentiation and its best to let your intuition guide you when talking about these concepts because "walking straight on a sphere" is imo clear enough.
A differentiable manifold holds the key. Start with a topological space. So the points in ℝ^3^ you described along with the by the ℝ^3^ induced topology is indeed the goto. Note that the radius of the sphere no longer matters as any sphere can be projected onto any other homeomorphically.
Then define homeomorphic maps from open subsets of the ℝ^2^ onto the sphere until its covered. At least two such maps are necessary. The key is now that the maps necessarily have to overlap on the sphere and we thus get maps from an open subset in the ℝ^2^ to another open subset of the ℝ^2^ by using one map go to the sphere and the inverse of another overlapping map to go back to the ℝ^2^. By requiring that these functions be diffeomorphic we transport the structure required for calculus to the sphere and we can talk about the curvature of a path. Then we can observe the existance of straight line by describing a path with no curvature on the sphere.
Because of the requirement of diffeomorphism the structure is unique, i. e. any other such structure can be diffeomorphically mapped to eachother and we can switch out maps as we please without changing any properties of the objects constructed.
By this I meant that if you take any projection of the sphere onto a flat surface, use it to project a line without curvature on the sphere to the flat surface the line thusly obtained will be curved w.r.t. the structure of the flat surface.
edit: this is obviously incorrect as any world map will show apologies. I should have said that there is a projection for any straight line on the sphere which will map it to a curved one in the 2d space.
You limit yourself by only thinking in euclidean geometry. Spherical geometry is a well defined mathematical concept and straight lines in this metric have the intuitive definition of being the shortest path between two points.
Yes, using lat, long, and radius is better than xyz on the earth - usually. But the radius, the 3rd dimension, changes by where you are because the earth isn't actually a sphere. On this path it would get longer until you reached the equator, shorter until the most southerly point then longer again until you hit NZ. It is a wavy line not a straight one. Again you're projecting 3d onto 2d (because you're incorrectly assuming a fixed radius) and saying that that error in projection doesn't matter.
The better visualization is here in that thread:
https://cdn.bsky.app/img/feed_fullsize/plain/did:plc:r643qxafn6b3pxfffiodojbn/bafkreibfe7ihvpro7hkjqygekbnt6iseefl7xchkroownxit576d3f3vze@jpeg
Thanks, turns out I can't undo a Mercator projection mentally.
Globes are trippy man, how do they work???
It's because this task understands "straight line" to mean "not having to change direction".
A "straight line on a curved surface" is called a geodesic. It's the path a tiny car would drive on the surface if you didn't move the steering wheel. Generally it's the shortest path between two points on the surface, although that definition gets iffy for long paths that start to loop back — obviously, going 90% of the way around the equator is longer than going 10% in the other direction, even though both paths would be geodesics. I prefer the car explanation.
The earth isn't a sphere though. Even if that has less error it is not none. A geodesic path would also not be straight because of the shape of the earth.
Also, you can define a geodesic for any surface, the concept isn’t specific to spheres.
Sorry, I shoul've said. The earth isn't a sphere, ellipsoid, or other regular geometric shape. The ocean's surface is less so and changes by the tides. Those shapes can work to model the surface locally and globally depending on accuracy needed but are inherently flawed.
Person 1: Does that matter? Person 2: No, let's just simplify. Person 1: Ok, well we can really simplify using a Mercator projection. Person 2: You're doing it wrong. We need to simplify the part that makes the line not straight, but not so much that it looks bendy again. Our projection needs to be at the level that makes the answer I want to be true look right. Person 1: Does the question even make any sense in this context then?
It doesn’t have to be a regular geometric shape. Any conceivable surface, no matter how awkward and lumpy — unless you have some infinitely rough mathematical object or other weird thing that doesn’t exist in real life — will permit the definition of geodesic curves.
But also, how much detail you account for is inherently a subjective decision tied to the level of precision you need for your specific application. Are you going to consider every whitecap and speck of foam when you describe your path? That depends! If your goal is to steer an ocean liner in a roughly straight line without hitting any landmasses, then probably not!
If you’re a satellite looking for sea-level defects due to gravitational anomalies, then you might need a little more precision.
The question asks for an approximate answer, so you can approximate the earth as a sphere. Your path will be roughly correct, since the earth’s deviation from being a sphere is extremely small, on the order of a few kilometers.
If you leave the UK headed southeast and keep a straight line, eventually you'll wind up back where you started (coming into the UK from the northeast), because the Earth is spherical. If you went due south, then eventually you'd pass through Antarctica and come out the other side heading north. But if your trajectory doesn't take you through the south pole, then you'll still come out headed north instead of south but at an angle. If you follow the red line after where it stops, it would go through Asia and get to the Arctic and then curve back south and that's how you'd wind up coming into the UK from the northeast. It looks like it turns but that's only because of how things change when you project a 3d sphere onto a 2d map.