So TL;DR, the XKCD method, but with six words instead of four and using a larger wordlist?
this post was submitted on 19 Jun 2024
110 points (99.1% liked)
Privacy
31876 readers
380 users here now
A place to discuss privacy and freedom in the digital world.
Privacy has become a very important issue in modern society, with companies and governments constantly abusing their power, more and more people are waking up to the importance of digital privacy.
In this community everyone is welcome to post links and discuss topics related to privacy.
Some Rules
- Posting a link to a website containing tracking isn't great, if contents of the website are behind a paywall maybe copy them into the post
- Don't promote proprietary software
- Try to keep things on topic
- If you have a question, please try searching for previous discussions, maybe it has already been answered
- Reposts are fine, but should have at least a couple of weeks in between so that the post can reach a new audience
- Be nice :)
Related communities
Chat rooms
-
[Matrix/Element]Dead
much thanks to @gary_host_laptop for the logo design :)
founded 5 years ago
MODERATORS
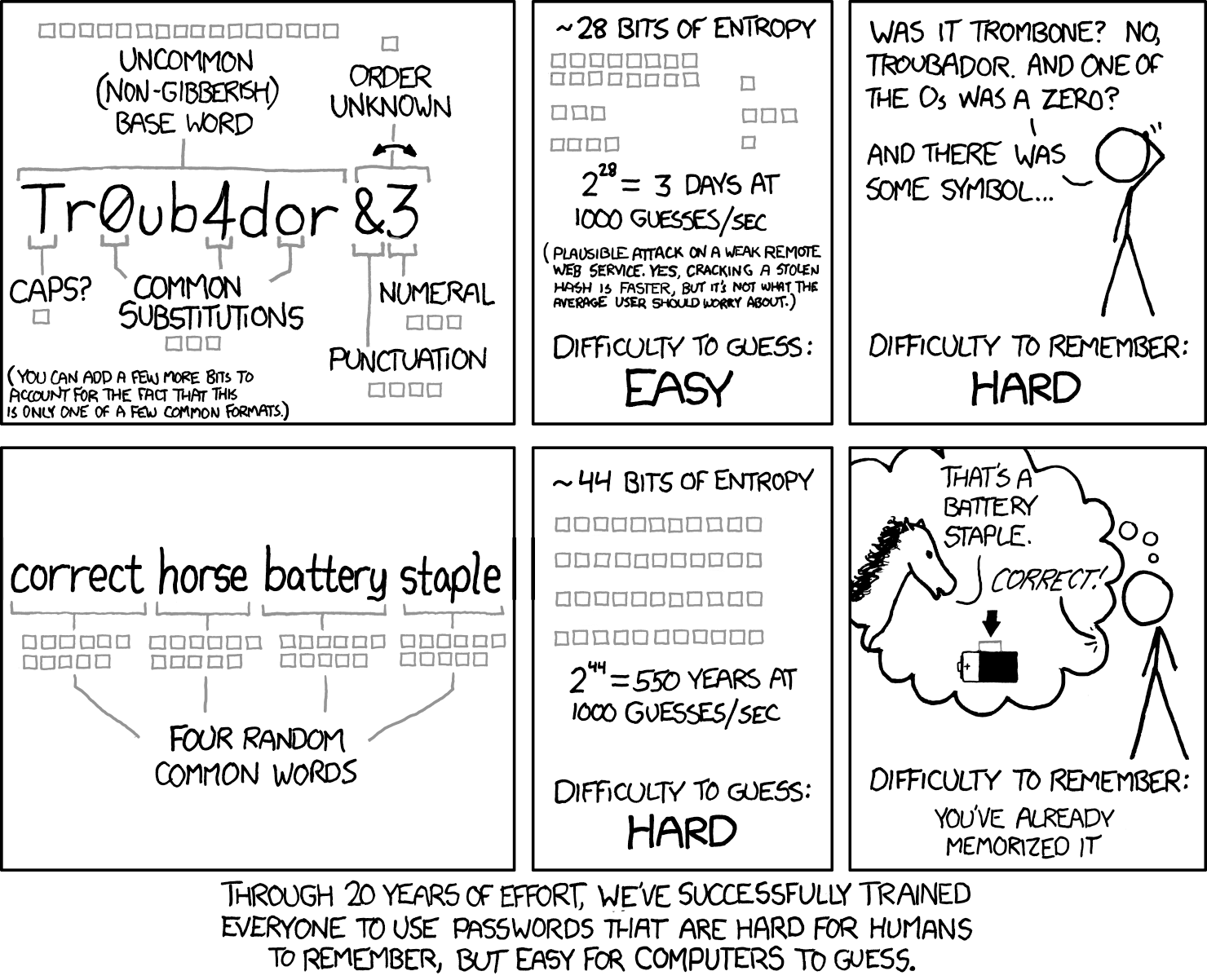
Nobody remembers diceware?
Eff has a better list imo. Diceware has a tonne of short abbreviations like "1st". Eff is words that are mostly 5 to 8 characters long. Much more xkcd like and easier to make a mnemonic out of.
I used to use it but have switched to using the first letter of each word in a phrase with some numbers and special characters thrown in. It's not as much typing and I can still get 128 bits of entropy and I can just as easily memorize it.
If it's from a memorable phrase, then the phrase has a lot of redundancy and it's hard to estimate the actual entropy. Generating a random phrase and writing it on a slip of paper works for me. Keep the paper in your pocket and refer to it when you need to, instead of trying to memorize it. Once you've typed it into the computer a few times, you remember it automatically. At that point you can swallow the paper or use your favorite alternate secure disposal method ;).
#!/bin/bash
head -$[$SRANDOM % `wc -l /usr/share/dict/words | cut -f1 -d' '`] /usr/share/dict/words | tail -1
It is a good technique to be sure, but I haven't found it useful in my everyday life. In practice 99% of my passwords are stored in my password manager. I only remember like 3 passwords myself. For those I want them to be easy to type as I do it semi-regularly (whenever I turn on my computer or phone, my phone sometimes re-verifies, ...). These may be slightly easier to remember but end up being much longer. I find that I don't have issues remembering the 3 passwords that I actually regularly type.
In fact I recently switched my computer passwords to be all lowercase, just to make it easier to type. I've offset this reduced entropy by making them longer (basically shift+key is similar entropy to key+key and easier to type, especially on phones or on-screen keyboards).
The recommended 6 words produces incredibly strong passwords. The equivalent with all lowercase would be 16.5 characters. Personally I went for 14 characters and in my threat model that is very very secure. But this will also depend on your attack model. If it is a disk encryption password or other case where you expect that the attacker can get the hash then it will depend on the strength of the hash and possible attacker's computing power. If it is protected by a HSM that you trust you can get away with short PINs because they have strict rate limits. Any decent online service should also have login rate limits reducing required entropy (unless the leak the hash without resetting passwords, then see the above point where the attacker gets the hash). All of my memorized passwords fall into the category of needing very strong security but I still found that remembering a random character password that only only took about a week when entering it once a day.
This is precisely for the master password of your password manager, the one you actually need to be highly secure but memorable
That or passwords that won't go there in practice, like computer boot passwords
Yeah, but my point is that I use my master password enough that random characters are still memorable while being faster to type. For me personally there isn't really a use case where the easier memorability is worth the extra characters to type. But of course everyone is different, so it is good that this system is laid out for them with a great guide.
I also think encryption password security depends heavily on the hash. A hash that's takes along time to break will be more secure and will require a shorter password to be secure
Yeah, that is what I meant by "strength of the hash". Probably should have been more clear. Basically the amount of resources it takes to calculate the hash will have to be spent by the attacker for each guess they make. So if it takes 1s and 100MiB of RAM to decrypt your disk it will take the attacker roughly 1s and 100MiB of RAM for each guess. (Of course CPUs will get faster and RAM will get cheaper, but you can make conservative estimates for how long you need your password to be secure.)
Parallelism 1, iterations 15, memory 512mb
New status unlocked! LUNATIC
Keep in mind they will be using GPUs with lots of ram and cores so that 1s will be more like hundreds or thousands a second.
It depends a lot on the hash functions. Lots of hashes are believed to be difficult to parallelize on GPUs and memory hard hash functions have different scaling properties. But even then you need to assume that an adversary has lots of computing power and a decent amount of time. These can all be estimated then you give yourself a wide margin.
Neat, and if you want a physical item to prompt you to do so https://www.crowdsupply.com/dicekeys/dicekeys can be an interesting option.
If you haven’t got any dice handy you can use random.org to generate the numbers for you. Or even select a set of words from the list
select a set of words from the list
I would be very careful doing this. It is very easy to introduce significant bias. Humans are terrible at picking random numbers.
If you can't find dice I would recommend:
- Having a computer pick random items for you.
- Renumber the list into binary and flip a coin 12 times for each word. (This results in a slightly shorter word list but should be string enough).
I meant use random.org select the words directly rather than go through the steps of getting numbers and then lookup.
I get the bias. A big weakness in the one time pads from WW2 was the word callers putting words back they thought were too frequent :)
Shameless self-plug: if you want something without Cloudflare in front of it dicewa.re is nice. Keep in mind though that in general it is not recommended to rely on random number generators as their source of randomness cannot be verified.
Doesn't using a particular wordlist limits choice, gives attackers a wordlist to generate the password from
Nope, As long as you're not as uncreative as to use Correct Horse Battery Staple.
Well it still technically does give them a list, it's just that even with the list there are a lot of combinations.
Technically, yes. But the article already mentioned the amount of effort for the brute force to succeed (that is, practically never, if the phrase is truly random.)
But anyway. With regular passwords, the attackers already have a list: the alphabet plus numbers and symbols. Not really that different.
Even a "traditional" password would have a "list" that attackers could know (all the possible characters that can be used in a password), now compare this set of +-150 characters with the set of possible words that can be used (probably close to 250k per language if you take out some similarities).
Even with only 4 words, the number of possibilities is astounding.
Technically yes. But the method is by far strong enough that this isn't an issue. This is sort of always the issue with calculating entropy. We say that password has less entropy than 8(A>Ni'[. But that is baking in assumptions about the search space. If password is a randomly generated string of lower, upper, numbers and symbols it is just as secure as the latter. (80^8^ ≈ 10^15^ candidates) but if password was generated as just lowercase characters it is far less secure (26^8^ ≈ 10^11^ candidates) but if it was a random dictionary word it is not very secure at all (≈ 10^5^ candidates) and if it was chosen as one of the most popular passwords it is even less secure. How can one password have different entropy?
The answer is basically it matters how the attacker searches. But in practice the attacker will search the more likely smaller sets first, then expand to the larger. So the added time to search the smaller sets is effectively negligible.
What may be more useful is the "worst case" entropy. Basically the attacker knows exactly what set you picked. For the password case that is 1 because I just picked the most common password. For the rolling method described above it is 6^5^6^ ≈ 10^23^ because even if they know the word list they don't know the rolls. You may be able to go slightly higher by building your own word list, but the gains will probably be fairly small and you would likely get far more value just by rolling one more word on the existing list than spending the time to generate your own.
1200*1200*1200*1200*1200*1200 is a lot of combinations
It does limit choice, but so long as you aren't retaining the generation list somewhere an attacker can find it, how are they to know your list? As long as your list is incorporating less common words, your attacker can't even simplify the problem by focusing on the most common words. Just one rare word can expand the list they need to use by tens of thousands of words.
Yes, but when the list is long enough and you have enough words, it is to difficult to guess.
Think about it. The list of all possible characters is also known, still with enough length and randomness it becomes too difficult to guess too.
Just mispel a word, replace a vowel with a numb3r and the wordlist is useless