this post was submitted on 20 Aug 2024
756 points (97.2% liked)
Memes
45745 readers
1860 users here now
Rules:
- Be civil and nice.
- Try not to excessively repost, as a rule of thumb, wait at least 2 months to do it if you have to.
founded 5 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
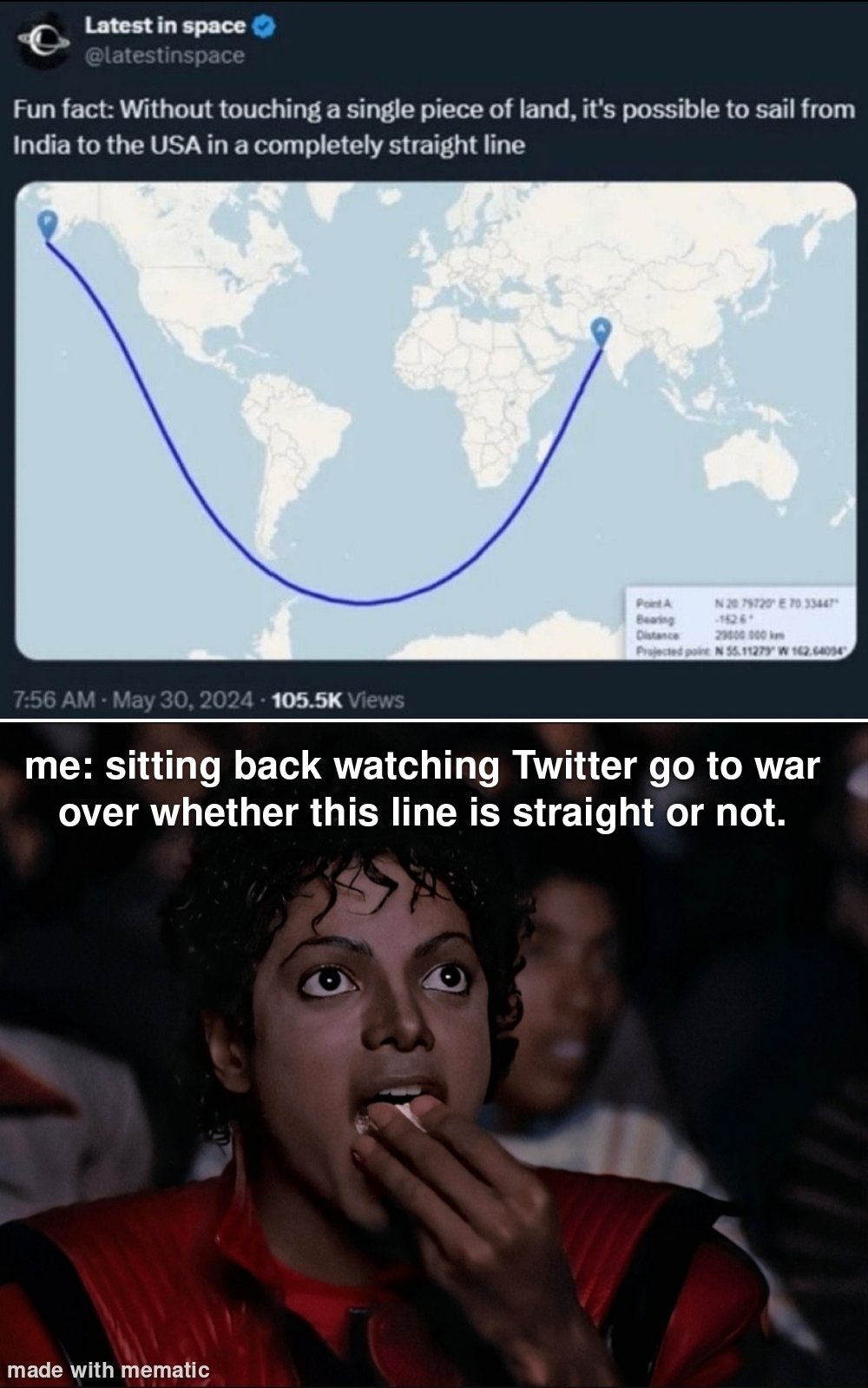
You are absolutely correct, but to add on to that even more:
When we talk about space, we usually think about 3D euclidean space. That means that straight lines are the shortest way between two points, parallel lines stay the same distance forever, and a whole bunch of other nice features.
Another way of thinking about objects like the earth is to think of them as 2D spherical manifolds. That means we concern ourself only to the surface of the earth, with no concept of going below the surface or flying up into the sky. In S2 (that's what you call a 2D spherical manifold), and in spherical geometry in general, parallel straight lines will eventually cross, and further on loop back and form a closed loop. Sounds weird, right? Well, we do it all the time. Look at lines of Longitude, for example.
We call the shortest line connecting two points in curved manifolds geodesics, as you said, and for all intents and purposes, they are straight. Remember, there is no concept of leaving the sphere, these two coordinates is all there is.
What one can do, if one wants to, is embed any manifold into a higher-dimensional euclidean one. Geodesics in the embedded manifold are usually not straight in higher-dimensional euclidean space. Geodesics on a sphere, for example, look like great circles in 3D.
Absolutly fantastic explination of how to conceptualize the complexities of geometry. Such an interesting area of mathematics