this post was submitted on 01 Dec 2023
48 points (98.0% liked)
Learn Programming
1625 readers
1 users here now
Posting Etiquette
-
Ask the main part of your question in the title. This should be concise but informative.
-
Provide everything up front. Don't make people fish for more details in the comments. Provide background information and examples.
-
Be present for follow up questions. Don't ask for help and run away. Stick around to answer questions and provide more details.
-
Ask about the problem you're trying to solve. Don't focus too much on debugging your exact solution, as you may be going down the wrong path. Include as much information as you can about what you ultimately are trying to achieve. See more on this here: https://xyproblem.info/
Icon base by Delapouite under CC BY 3.0 with modifications to add a gradient
founded 1 year ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
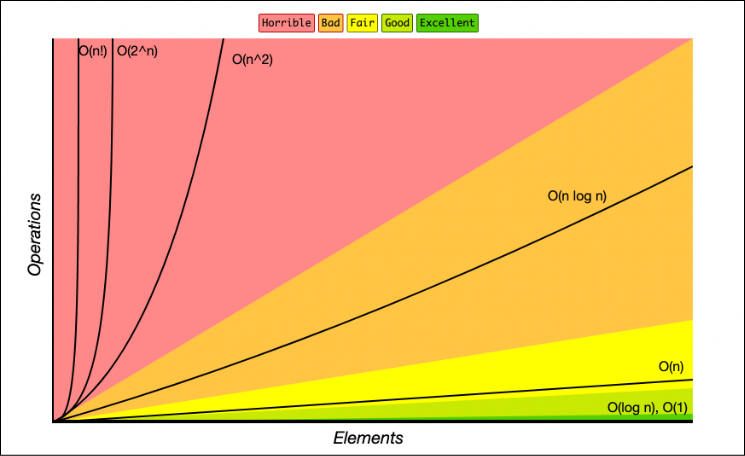
Except the point of this post is that a different sort with worse Big O could be faster with a small dataset.
The fact that you're sorting those 64 ints billions of times simply doesn't matter. The "slower" sort is still faster in practice.
That's why it's important to realize that Big O notation can be useless for small datasets. Because it can actually just be lying to you.
It's actually mathematical. Take any equation:
y = x^2 + xFor large x the squared term dominates. The linear may as well not exists. It's O(x^2). But when x is below 1? Well suddenly that linear term is the more important one! Below 1 it's actually O(x) in practice.