this post was submitted on 20 Aug 2024
756 points (97.2% liked)
Memes
45724 readers
1049 users here now
Rules:
- Be civil and nice.
- Try not to excessively repost, as a rule of thumb, wait at least 2 months to do it if you have to.
founded 5 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
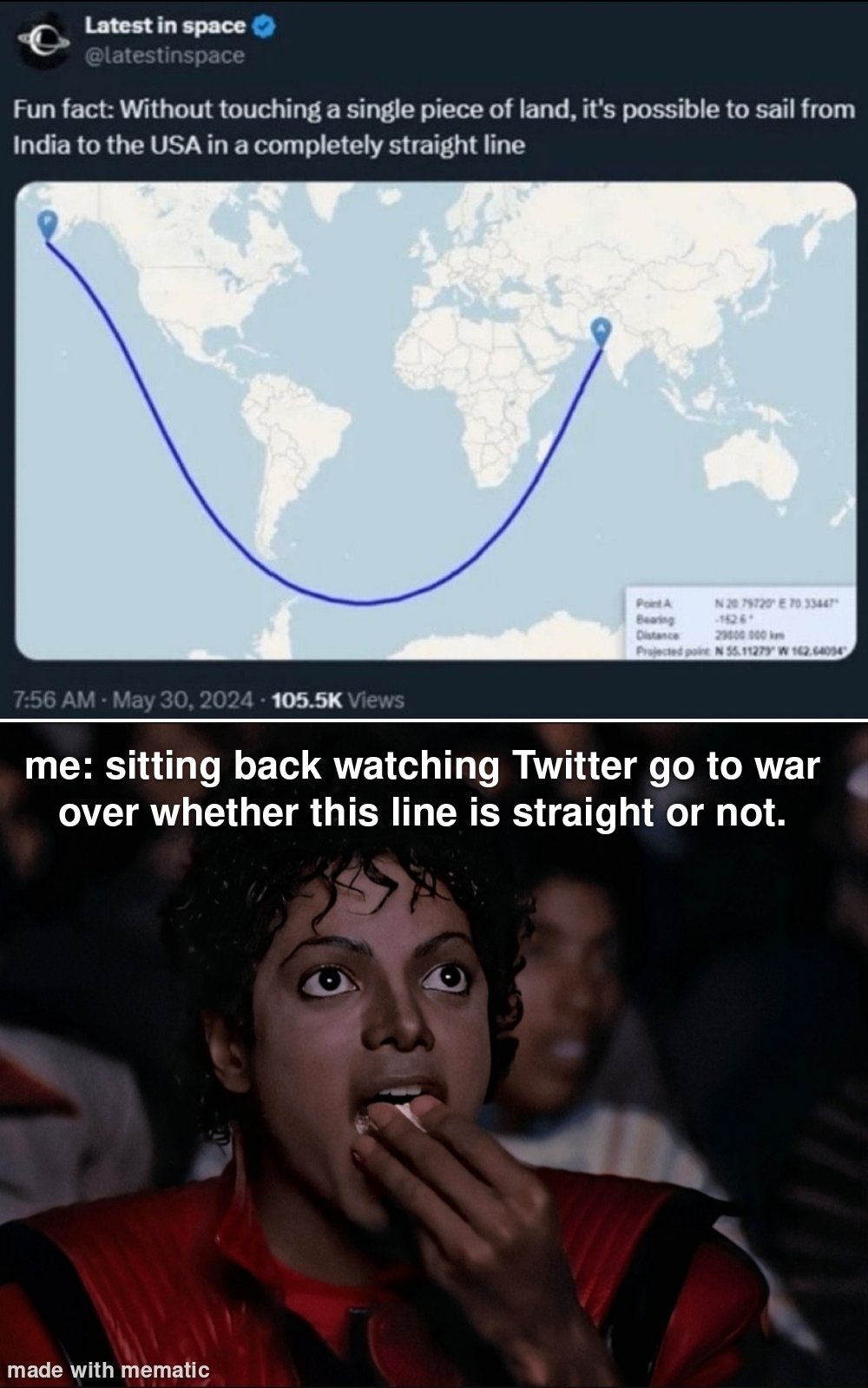
I feel like this is related to the can't measure the coast' thing.
Like if you zoom in enough you are always traveling in a straight line.
You just discovered the field of calculus! If you look closely enough at any smooth function it looks locally linear, and the slope of that linear function is it's derivative
Not quite what's happening here, here the problem is if you consider geodesics on a sphere to be straight. In special geometry they are, for all intents and purposes, but in higher euclidian geometry they form large circles
I don't know... straight, I would assume, means that I could walk or drive a vehicle and not turn at all, ignoring any external influences like waves and currents in this case.
But your vehicle would itself "curve" "downwards" due to gravity, surely a straight line means that you can point a laser, or a hypothetical 0 mass particle beam, uninterrupted from your starting point to your destination.
Depends on your frame of reference. When traversing the surface of a globe, your described concept of a straight line isn’t intuitive.
in ur every day life if u travel in a car without changing direction would u say that u went in a straight line or in an arc. Clearly u are just trying to be a pedantic cunt for no reason.
It's more that 2d projections of 3d objects are wonky and unintuitive.